方程式の問題の場合、計算をひたすら解いていくというのも1つの手ですが、空間座標に落とし込める事ができるのであれば、図を書いて視覚に落とし込むのも、1つの手です。
両方の方法を習得された方が、解答方法に幅がでますので、よいかと思います。個人的には後者の図に落とし込んで考える方が好みです。理由は、図に書くと一目瞭然で、しかもちょいミスが少なくなると思っているからです。
問題1:以下の2次方程式の解が異なる2つの正の解をもつとき、定数aの値の範囲を求めよ。
解法1(計算式を解いていく方法):
2つの異なる実数も持つことより、判別式Dは、D>0
すなわち
\( \qquad \qquad D/4 =\left( a-3\right) ^{2}-\left( a+3\right) = a^{2} -7a + 6 > 0 \) ・・・①2つの解をα、βとすると、解と係数の関係より、α>0、β>0の条件から
\( \qquad \qquad \alpha +\beta =-2 \left( a-3\right) >0 \) ・・・② \( \qquad \qquad \alpha \beta = a+3 > 0 \)・・・③解法2(図を書く方法):
与式を変更すると
\( \qquad \qquad y=\left\{ x+\left( a-3\right) \right\} ^{2}-\left( a-3\right) ^{2} + a + 3 \)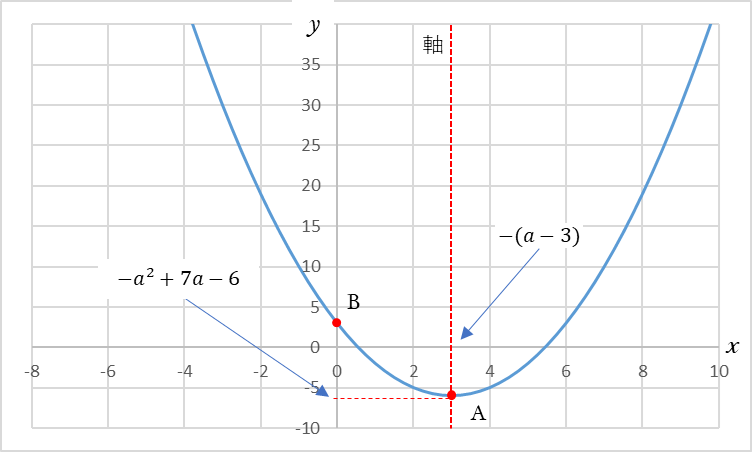
④式を図にしたものが上図です。ポイントは2次関数の頂点である点Aとy軸との交点Bです。
異なる2つの正の解を持つという事は、④とX軸の交点α、βが正であることを意味します。これは、Aのx座標(軸のx座標)は正である必要があります。また、下凸のグラフであるから軸の頂点であるAのy座標は、負である必要があります。それぞれ式に表すと、
\( \qquad \qquad -(a-3) > 0 \)・・・⑤ \( \qquad \qquad -a ^{2} + 7a -6 < 0 \)・・・⑥x=0である点Bのy座標は、条件から正である必要がありますので、
\(\qquad \qquad a+3 > 0 \)・・・⑦⑤式は②式の両辺を2で割れば同じになり、この事は軸のx座標がα、βの中点を意味しています。別の見方をすれば、軸を中心に2次関数は左右対称であることを物語っています。また⑥式は①式の判別式に相当し、⑦式は③式に相当します。あとの計算結果は、解法1と同じになります。
図を書くことで、数式が持っている意味が浮かび上がってくる感じがしませんか。
ここで、もう一問。
問題2: 次の2直線の交点の軌跡を求めよ。但し、mは実数全体とする。
\( \qquad \qquad mx - y = 0 \)・・・➉ \( \qquad \qquad x + my - m -2 = 0 \)・・・⑪解法: 工夫して数式を変形していけば、解けますが、ここでは図に落とし込むという事を考えたいと思います。mは実数全体ですので、適当な値を1つ入れても成立します。そこで、値を一つ入れてまずは図に書いてみましょう。例えば、簡単な処で、 x=1を代入してみます。その図が下図になります。直線が直交している事に気が付くと思います。(気づいてほしい。。。)
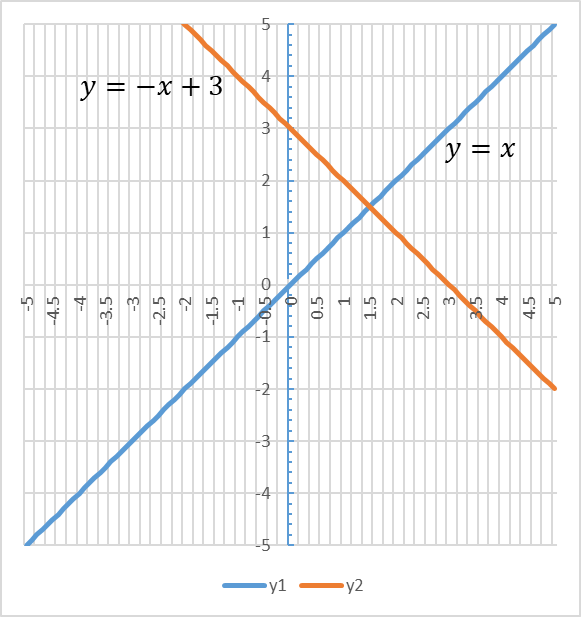
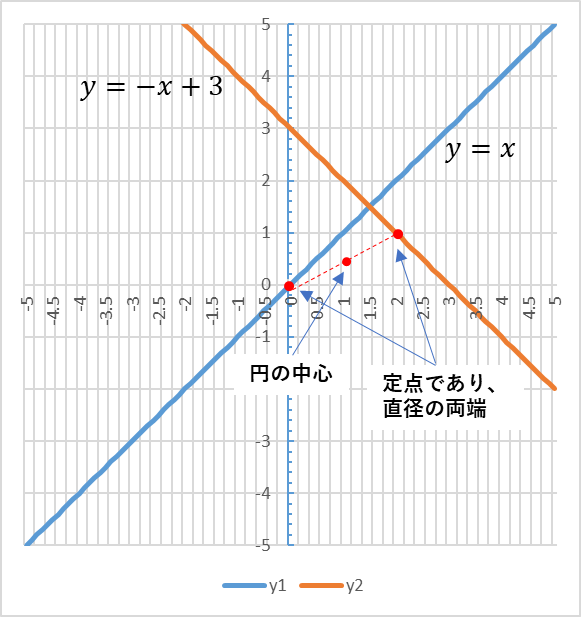
再度➉、⑪式をよく見ると、それぞれの傾きから直交している事が分かります。➉式のmの値を大きくしても、それに追従して⑪式の傾きも変化して、直交している状態は変わりません。
ここで更に気が付いてほしい事は、➉式のmを変化しても、ある定点を通ることです。それは原点です。➉式をmの恒等式と考えれば、(0,0)を絶えず通るわけです。そうすると、⑪式はどうなのだろうという疑問がわきます。同様に、mの恒等式と考えれば、
\( \qquad \qquad x - 2 + m \left( y - 1 \right) = 0 \)・・・⑪’となり、(2,1)を通ることが分かるわけです。2つの直線がそれぞれある定点を通り直交する事の意味するところは、2直線の交点は、この定点を直径の両端とした円の軌跡を意味します。この円の軌跡を数式化すれば、それが答えになります。
図を書くことで、それぞれの式の意味を理解できて、問題作成者の意図が見えてくるわけです。