生徒さんを教えていた時になるほど、そういったアプローチもあるのだなと思った事がありましたので、ここで紹介したいと思います。基本的な対数の計算問題ですが、ちょっとした心構えをお伝えしたいと思います。
【問題】次の方程式を解け。
\( \log _{3}x+\log _{3}\left( x-2\right) =1 \)【解答】
オーソドックスには次のような手順の解法になるかと思います。
真数条件より、
\( x > 0 かつ x-2 > 0 より、 x>2 \) ・・・① 底をそろえて、\(\log _{3}x(x-2) = \log _{3}3 \) ・・・② ②式より、\(x\left( x-2\right) =3 \) ・・・③ ③式を変形していき、 \( x^{2} - 2x - 3 = 0 \)、\( (x-3)(x+1) = 0 \) よって \( x=3, -1 \) ・・・④ ①,④より \( x=3 \) これが解答になります。ここで、ほんのちょっと違う計算処理です。
真数条件までは同じですが、②から③での計算がほんの少し違います。問題の式を見ると、中学校で行った時の因数分解を思い出すのではないでしょうか。そうすると、ごく自然に右辺を0にするという式変更を行うと思います。
\( \log _{3}x+\log _{3}\left( x-2\right) - 1 = 0 \)底をそろえて、対数の公式を使用して変更する次のようになります。
\( \log _{3}x+\log _{3}\left( x-2\right) - \log _{3}3 = 0 \) \( \log _{3} \dfrac{x\left( x-2\right) }{3} = 0 \) ・・・⑤ここで鉛筆が一瞬、止まってしまうかもしれませんが、対数を取った時に0になるはグラフから分かるように真数が1の時です。結局、低をそろえることになりますが、次のような式になります。
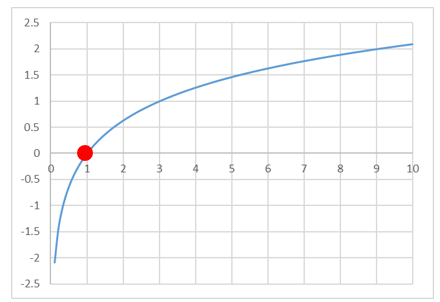
ここでお伝えしたかった事は、式変形自体は公式にのっとって行っており、等価なものです。そうすると、この式変形でも解けるという、ある意味確信をもって解いていって欲しいということです。自分の解き方は問題ないという自信です。こういった経験を踏まえた上で、最初に述べたオーソドックスな手順で解答するようになっていくのはいいと思います。ただ、自分で解答しようとした方法が2番目に紹介した手順で、解答の途中で諦めて、参考書などの解答を見て、解答方法を覚えるというのは感心できません。それぞれの問題に対して、解き方を暗記するという行為につながりかねず、数学も色々と暗記しないといけないという錯覚、思い込みに陥るからです。(この解答された生徒さんは、最後までしっかりと解答されていました。)
蛇足ですが、そもそも、対数とはなんであったかと考えると、
下式のように、指数関数で表現されたものを単純に対数関数に置き換えただけです。
\( Y = a^{X} <=> X = log _a{Y} \) ⑤式と \( X = log _a{Y} \) をにらめっこすると、 \( X=0, a = 3, Y=\dfrac{x\left( x-2\right) }{3} \) よって、 \( Y=a^{x} \) に代入すると、\( \dfrac{x\left( x-2\right) }{3} = 3^{0} \)これも③に戻ります。


