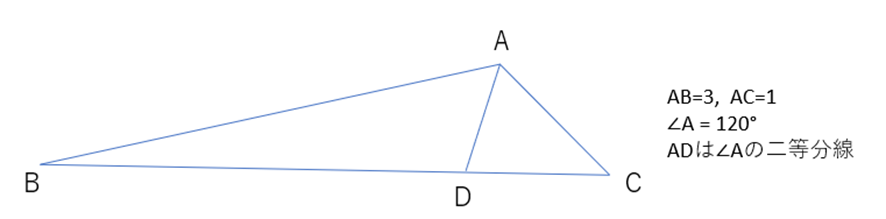
下記の図で、ADの長さを求めなさい。という問いに対して、面積を用いる方法と余弦定理を用いる方法の2種類あります。
面積を用いる方法だとあっさり解けてしまうので、ここでは余弦定理を用いて解くという条件のもと、解きたいと思います。
与えられた条件から、直ちにADを求めることはできず、次に目がいくのは、線分BCで、これは求めることはできるとすぐに分かります。更にDは∠Aの二等分線であるという条件から、下式より、BDおよびCDが求まります。
\( \qquad \overline{BC}^{2} = \overline{AB}^{2} + \overline{AC}^{2} – 2 \cdot \overline{AB} \cdot \overline{AC} \cdot \cos A \) \( \qquad \overline{BC} = \sqrt{13} \qquad ( \because \overline{BC} > 0 ) \) \( \qquad \overline{AB} : \overline{AC} = \overline{BD} : \overline{CD} \) \( \qquad \overline{BD} = \dfrac{3\sqrt{13}}{4} \)ここから解き方としては、2パターンに分かれるのではないかと思います。
解法1)
① 三角形ABCに着目し、∠B(または∠C)のCos Bを求める。
② 三角形ABDに着目し、ADを求める。この時、AD>0故、ADは一つだけ求まる。
①②を数式化すると、
\( \qquad \overline{AC}^{2}=\overline{AB}^{2} + \overline{BC}^{2} – 2 \cdot \overline{AB}\cdot \overline{BC}\cdot \cos B \) \( \qquad cosB = \dfrac{7}{2\sqrt{13}} \) \( \qquad \overline{AD}^{2}=\overline{AB}^{2} + \overline{BD}^{2} – 2 \cdot \overline{AB}\cdot \overline{BD}\cdot\cos B \) \( \qquad \overline{AD} = \dfrac{3}{4} \qquad ( \because \overline{AD} > 0 ) \)解法2)
① 三角形ABDに着目し、∠BADの情報から、ADを求める。しかし、この場合はADが2種類、算出される。
② 同様に三角形ACDに着目し、∠CADの情報から、ADを求める。これも2種類のADが求まるが、①との共通の解となるものを求めて、最終的な解とする。
①②を数式化すると、
\( \qquad \overline{BD}^{2}=\overline{AB}^{2} + \overline{AD}^{2} – 2 \cdot \overline{AB}\cdot \overline{AD}\cdot \cos 60 \) \( \qquad \overline{AD} = \dfrac{3}{4}, \dfrac{9}{4} \) \( \qquad \overline{DC}^{2}=\overline{AC}^{2} + \overline{AD}^{2} – 2 \cdot \overline{AC}\cdot \overline{AD}\cdot \cos 60 \) \( \qquad \overline{AD} = \dfrac{3}{4}, \dfrac{1}{4} \)解法1の場合は、ADは1つ算出されるが、解法2の場合は途中、ADは2種類算出されますが、これはどういうことなのでしょうか。
結論から言うと、三角形の合同条件と関連します。三角形の合同条件は、
- 3辺がそれぞれ等しい。
- 2辺とその間の角がそれぞれ等しい。
- 1辺と両端の角がそれぞれ等しい。
解法1では、AB、BD、∠Bの情報からADを求めましたが、これは三角形の合同条件の“2辺とその間の角がそれぞれ等しい”に相当する情報を使用しADを求めています。
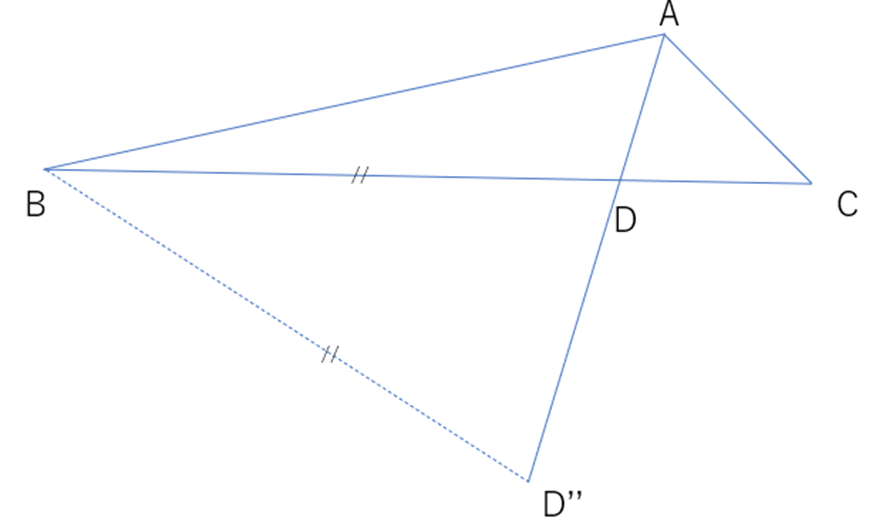
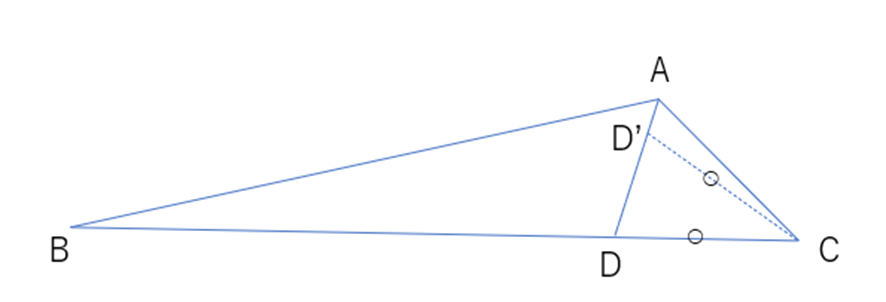
しかし、解法2では三角形の合同条件に該当する情報から求めていません。使用する情報が完全に意図した三角形を再現する情報でなかったために2種類の三角形がでてきてしまったのです。それが下の図にあたります。三角形ABDおよび三角形ABD”、あるいは三角形ACDおよび三角形ACD’です。
単に、余弦定理の公式に数値を当てはめて計算をすればよいという考えでいると、解法2の場合は、2種類の解を求めて、それを最終的な解答してしまう恐れがあります。
限られた時間で、問題を解かなくてはならない状況下では、今回のような考察をするのはなかなか難しいのですが、少なくとも解が2つでてきた段階で、“どうしてだ?これは正しいか?”という疑問をもつことはとても大切です。


