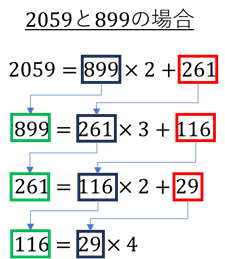
ユークリッドの互除法は、整数a,bの最大公約を求める手法として、以下のStepを踏み、そして説明として簡単な計算例が示されます(この例の場合、最大公約数は29となります)が、直感的に分かりづらい人もいるかもしれません。私が高校数学を学習した頃、このような事を習ったかなと考えつつ、私には少々わかりづらいものでした。
Step1: aをbで割った時の余りをrとする。
Step2: r=0ならば、bが最大公約数。
r>0ならば、aをbに、bをrに置き換えて、Step1に戻る。これをr=0になるまで繰り返す。
そこで、こんな風に考えるのはいかがでしょうか。辺a,bの長方形の図形を書き、次のようなStepを踏んでいきます。
Step1: “長辺” / “短辺” (長辺を短辺で割る)
Step2: 余った領域をまた“長辺” / “短辺”
Step3: 余った領域がなくなるまで繰り返す。
ここで簡単な例を。
例1) 最大公約数6である78と30の場合
図1-1で、“長辺” / “短辺”を行うと、30 x 30の正方形が2つできます。この作業は短辺の長さの正方形を切り出す作業でもあります。残りが余りとなります。この余りを図1-2で使うわけです。
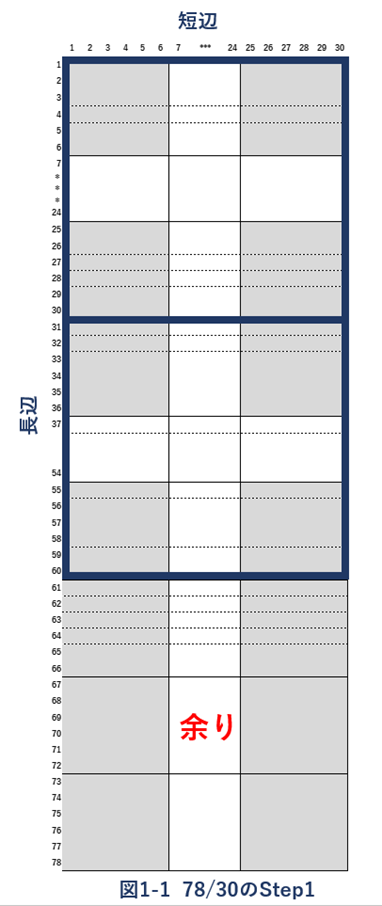
図1-2では、長辺と短辺が入れ替わります。図1-1で短辺であった“30”が、今度は長辺とし取り扱われます。今後、このように長辺と短辺が交互に入れ替わっていきます。
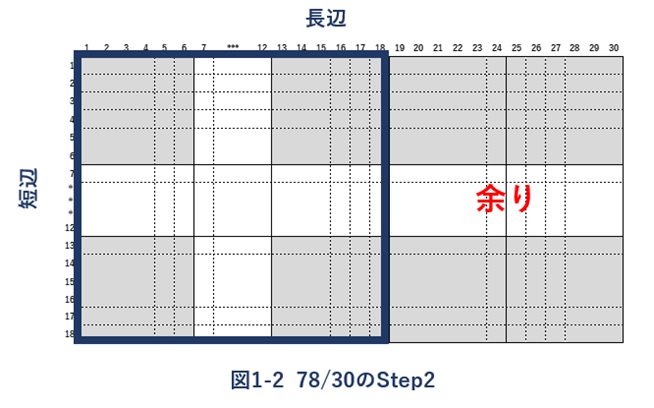
図1-3も、これまでと同様に行います。
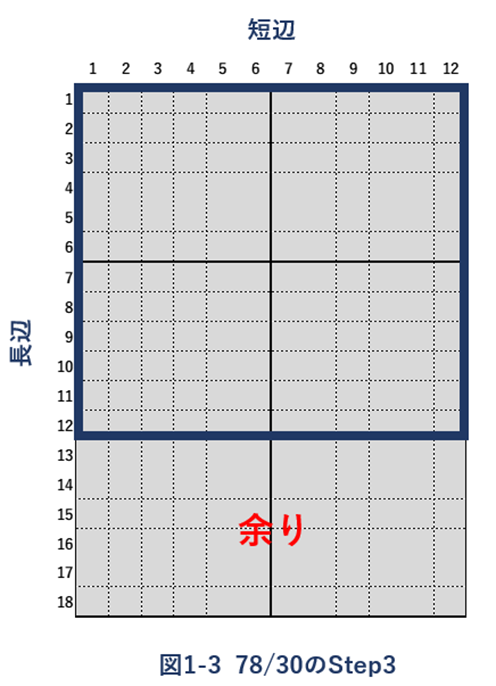
図1-4で、ようやく余りがなりました。この時の短辺が最大公約数(6)となるわけです。
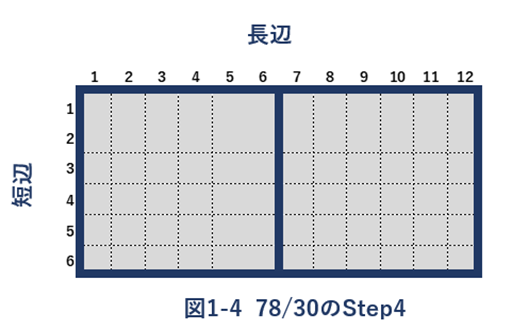
長方形が転がって転がって最終的に正方形になるような感じ(今回の場合、図1-4では正方形になりませんでしたが。。。)で、例えがあまりうまくはないのですが、ごつごつした石が川の流れの中で、転がって丸くなっていく感じでしょうか。
それでは、互いに素(最大公約数が1)の場合はどうでしょうか。
例2) 互いに素である12と7の場合
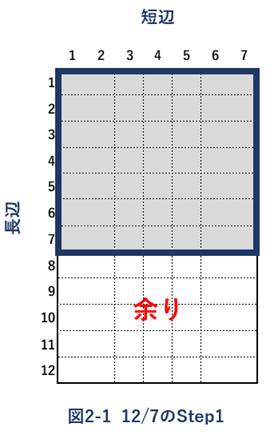
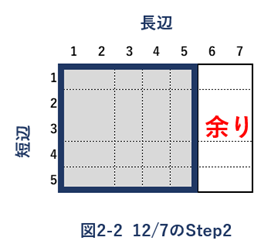
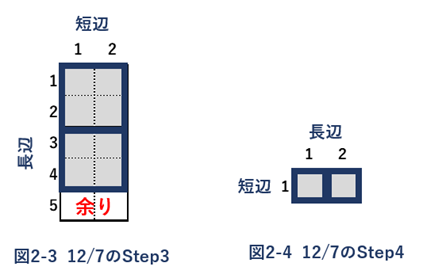
最終的に、図2-4で示されるように短辺が1となり、最大公約数が1であることが示されました。


