京都大学(文系)の数学の入試は、120分の試験時間で大問5問の構成です。
まずは、出題傾向を調べてみると、“微積”、“確率”、“ベクトル/図形”あたりは毎年のように出題される分野で、“整数問題”もよく出題されていることが分かります。1つの大問に2つの分野がある場合は、その設問に(1),(2)という具合に2問の小問に分かれていたということです。
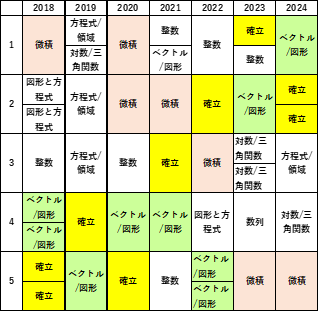
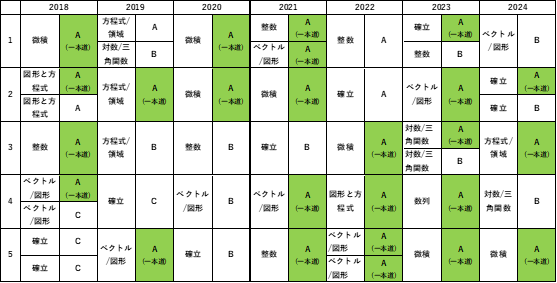
更に、各設問を解いてみると、難易度が全て同じ程度というわけではなく、相対的に易しいA問題から、結構難しいC問題に分かれることが分かります。その年、その年で全体的な難易度は違いますが、BからCレベルの問題が1、2問出題されている傾向があるようです。
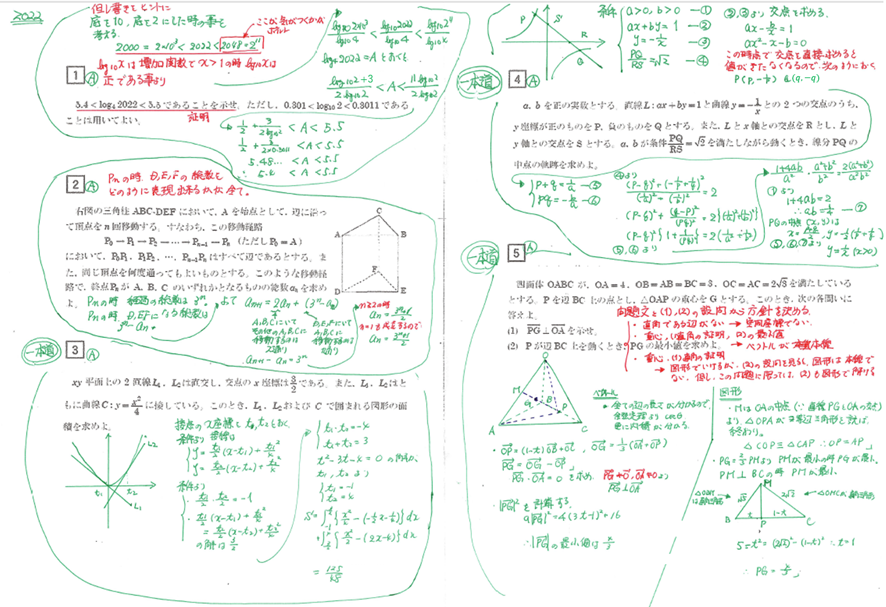
実際に入試問題をどのように解いていくのがよいか、検討する為に一つの例として、2022年度の問題を用いて、ちょっと考えることにします。
2022年度の問題は比較的、易しい問題が多かった年ですが、それでも試験会場での緊張した雰囲気、限られた時間内に解かなくてはならないというプレッシャーを考えると、易しい問題と言っても必ず解けるものではありません。
入試問題でそれなりの得点を得るには、それなりの戦略は必要かと思います。
その一つとして、難しい問題と易しい問題との切り分けです。
受験生の心理状態を考えると、難しい問題を解かないと合格できないと思っている方もいるかと思いますが、むしろ易しい問題をしっかり解ききることの方が合格への近道だと思っています。難しい問題を解けたときは、受験生にとってはかなりの達成感があるかと思いますが、易しい問題の途中で計算ミスをしていたら目も当てられません。難しい問題を完全正解しても易しい問題を完全正解しても、どちらも点数は全く変わらないのですから。
そのようなことから、一つの戦略として、難易度が高い問題に時間をかけるよりも、比較的易しい問題を解く時間をしっかり確保することが大切だと思っています。
そういった意味では、難しいか易しいかの切り分けをするということは非常に大切のように思えます。
最初の設問[1]は、比較的易しい問題になっている傾向にあり、また微積問題も比較的易しいようです。
数学は設問に記述されている条件と数学的知識でもって答えを出していきますが、この時に与えられた条件をどう処理するか、複数考えられる場合はどの道を選択するか悩ましいところです。しかし、その道がどう考えても一本しかない“一本道”の場合は、あとは計算問題みたいなものですから、確実に得点したいところです。2022年度の問題では、個人的には[3],[4],[5]の設問が、それにあたると思っています。
先ほどの表に難易度Aの下に“一本道”と書いたものはそれにあたります。
次に難しい問題ですが、
10分考えても、解き方が思いつかないような難しい問題は、試験時間以内では正答へはたどり着かないと諦めてしまって、その問題への意識を変えます。その問題は満点をとるのではなく、10%程度の得点を狙っていく。与えられた条件から、最初のステップでは必ず、皆、こう展開していくであろうという事を記述して、1点でも多く得点を得るように体裁を整えていくのも手かと思います。受験生の方には、この1点の重みを是非ともしっかり認識しておいて欲しいところです。合格ラインをその1点で越えるか、越えないかはとても大きいものです。
個人的な感覚ですが、Aが8割、Bが4割、Cが1割程度解けると合格者の数学平均点レベルに到達するのではと思っています。この得点率から言っても、Aレベルに時間を割く方が全体的なバランスを考えるとよいかと思います。
最後は計算ミスです。
易しい問題で計算ミスをして正答にならなかったという事は是非とも避けたいものです。特に、解答の最初の方で計算ミスをするとその後の話の展開に矛盾が生じる場合があり失点が大きくなり、目も当たられません。例えば、面積を求める積分の問題で、最後の最後の積分の計算で計算ミスするのは失点が小さくて済みますが、序盤から中盤にかけての積分範囲の決定や、場合分けし積分する式を導き出す過程での計算ミスは失点が大きいと思います。
解答の筋道がしっかりしている問題では、序盤から絶えず、計算が正しいかのチェックをしていきたいところです。
あと、証明問題は解答までたどりつけば、基本的に見直す必要ない(計算ミスがないから証明できた。)問題ですのでこれも、出来る限りものにしたいところです。


